প্রাচীন জনপদ আলেক্সান্দ্রিয়া

বোঝার জন্য প্রথমে এই ছবিটার (ছবি ১) দিকে তাকানো যাক। এখানে খ-গোলকের (Celestial Sphere) মধ্যে পৃথিবী ও সূর্যকে দেখানো হয়েছে। আকাশ সম্পর্কিত কিছু বোঝাতে আমরা খ অক্ষরটা ব্যবহার করি। যেমন, পাখি আকাশে ওড়ে বলে তাকে খেচর বলা হয়। তেমনিভাবে আকাশের গোলকটাকে বলা হয় খ-গোলক(Celestial Sphere)। আমাদের কাছে মনে হয় সবগুলো তারা খ-গোলকে প্রোথিত আছে যেটা এই ছবিতে আরও স্পষ্ট। এখানে (ছবি ২) সূর্য আকাশের তলের যে অঞ্চলে চলাফেরা করে সেই অঞ্চলের তারা এবং তারামণ্ডলগুলো(constellations) দেখানো হয়েছে। এই অঞ্চলে মোট ১২টা তারামণ্ডল আছে যাদেরকে রাশি(zodiac constellations) বলা হয়। কুসংস্কারে বিশ্বাসীরা মনে করেন মানুষের নিয়তির উপর এই ১২টি রাশির হাত আছে। ১২টি রাশি ঠিক ই আছে কিন্তু এদের গতিপথের সাথে মানুষ, প্রাণের অস্তিত্ব, নিয়তি এর সম্পর্ক নেই।
পৃথিবীর গতি(Motion of Earth):
এখন আমরা পৃথিবীর গতি নিয়ে আলোচনা করবো । পৃথিবীর গতি আছে দুই রকমের- আহ্নিক গতি (Daily Motion) ও বার্ষিক গতি(Yearly Motion)। পৃথিবী নিজের অক্ষের সাপেক্ষে ২৪ ঘণ্টায় একবার ঘুরে আসে যাকে বলা হয় আহ্নিক গতি। ২৪ ঘণ্টায় এক দিন হয়, দিনের প্রতিশব্দ অহ্ন যেখান থেকে আহ্নিক কথাটা এসেছে। এটা হচ্ছে (ছবি ১) পৃথিবীর ঘূর্ণন অক্ষ। এই অক্ষের সাথে লম্বভাবে যে তলটা আছে, তা খ-গোলককে ছেদ করলে যে বৃত্তটা তৈরি হয় তার নাম খ-বিষুব। এই ছবিতে ব্যাপারটা আরও স্পষ্ট বোঝা যাচ্ছে। এখানে খ-গোলকে আঁকা এই নীল বৃত্তটাই খ-বিষুব(Celestial equator)। তো ঘূর্ণন অক্ষের সাথে লম্বালম্বি এই তলটা পৃথিবীকে ছেদ করলে পৃথিবীর পৃষ্ঠে যে বৃত্তটা তৈরি হয় তার নাম বিষুব রেখা, এই ছোট সবুজ বৃত্ত দিয়ে এটা দেখানো হয়েছে। বিষুবরেখার উত্তরে পৃথিবীর উত্তর গোলার্ধ আর দক্ষিণে দক্ষিণ গোলার্ধ। বিষুব রেখার উত্তর দিকের কৌণিক দূরত্ব নির্দেশ করা হয় অক্ষাংশের মাধ্যমে, নাম থেকেই বোঝা যাচ্ছে এটা অক্ষের অংশ। আর বিষুবরেখা বরাবর দূরত্ব নির্দেশ করা হয় দ্রাঘিমাংশ দিয়ে।
এবার আসি বার্ষিক গতির কথায়। লাটিমের মত প্রতিদিনে একবার ঘুরতে ঘুরতে পৃথিবী সূর্যের চারদিকেও আবর্তন করে। সূর্যের চারদিকে একবার ঘুরে আসতে তার ১ বছর অর্থাৎ প্রায় ৩৬৫ দিন সময় লাগে। এটাই বার্ষিক গতি। এটা পৃথিবীর কক্ষপথ। এই কক্ষপথ যে তলে অবস্থিত তার নাম ভূকক্ষ। এখানে দেখা যাচ্ছে এর আরেকটা নাম সূর্যপথ। কারণটাও বিস্ময়কর কিছু না। যদিও পৃথিবী সূর্যের চারদিকে ঘুরছে, পৃথিবী থেকে আমাদের মনে হয় আকাশে সূর্যটা ঘুরছে। সূর্য প্রতিদিন পূর্বে উদিত হয়ে পশ্চিমে অস্ত যাচ্ছে। আবার বছরের একেক দিন সূর্য একেক স্থানে উদিত হচ্ছে। সুতরাং সূর্যের একটা আপাত বার্ষিক গতি আছে, যেটা ভূকক্ষ বরাবর। পৃথিবীর কক্ষপথের তল এবং পৃথিবীর সাপেক্ষে সূর্যের গতিপথের তল একই, তাই এটাকে ভূকক্ষও বলা যায় আবার সূর্যপথও বলা যায়। এই ছবিতে (ছবি ২) ব্যাপারটা আরও স্পষ্ট। এখানে ছোট লাল বৃত্তটা পৃথিবীর কক্ষপথ আর খ-গোলকে যে বড় লাল বৃত্তটা দেখা যাচ্ছে সেটাই ভূকক্ষ বা সূর্যপথ। বোঝাই যাচ্ছে সূর্যপথ ১২টি রাশির মধ্য দিয়ে অতিক্রম করে। পৃথিবী যখন এখানে থাকে তখন খ-গোলকের পটভূমিতে সূর্যকে দেখা যায় এখানে, এই তীর চিহ্নের শেষ প্রান্তে। আবার পৃথিবী যখন এখানে থাকে তখন সূর্যকে দেখা যাবে এখানে। এভাবেই খ-গোলকে সূর্যপথ তৈরি হয়।
তো এই দুটো ছবি (১ ও ২) থেকে আরেকটা বিষয় স্পষ্ট- তা হল পৃথিবীর ঘূর্ণন অক্ষ ভূকক্ষের দিকে একটু হেলে আছে। ভূকক্ষের উপর যদি একটা লম্ব রেখা টানা হয় তাহলে উত্তর ভূকক্ষীয় মেরু এবং দক্ষিণ ভূকক্ষীয় মেরু পাওয়া যাবে। সেক্ষেত্রে এই উল্লম্ব রেখাটার সাথে ঘূর্ণন অক্ষ প্রায় সাড়ে তেইশ ডিগ্রি কোণ(23.5 degree) করে থাকবে। এটা সত্যি হলে, সংজ্ঞা অনুসারে খ-বিষুব ও ভূকক্ষের মধ্যবর্তী কোণও সাড়ে তেইশ ডিগ্রি হওয়ার কথা। ছবি থেকে স্পষ্টই দেখা যাচ্ছে বাস্তবে আসলেই তাদের মধ্যবর্তী কোণ প্রায় সাড়ে তেইশ ডিগ্রি। এই ছবিতেও ব্যাপারটা খুব স্পষ্ট। এখানে নীল ও লাল বৃত্তের মধ্যবর্তী কোণ ২৩.৪ ডিগ্রি। এই কোণটাকে বলা হয় ক্রান্তিকোণ(titled angle)
ক্রান্তিকোণের কারণে কিন্তু সূর্যপথ এবং খ-বিষুব দুটো বিন্দুতে ছেদ করে, একটার নাম বসন্ত বিষুব, আরেকটা শারদীয় বিষুব। নাম থেকেই বোঝা যাচ্ছে একটা বসন্তকালে এবং অন্যটা শরৎকালে ঘটে। পৃথিবী সূর্যের চারদিকে বছরে একবার ঘুরে আসে। এই ছবিতে পৃথিবী যেখানে আছে সেটা বসন্তকাল, কারণ আমরা সূর্যকে এখন বসন্ত বিষুবে দেখতে পাচ্ছি। ঘুরতে ঘুরতে পৃথিবী যখন এখানে যাবে তখন সূর্যকে দেখা যাবে এখানে অর্থাৎ শারদীয় বিষুব বিন্দুতে। এই দুটো সময়ে পৃথিবী সূর্যের দিকে একটুও হেলে থাকে না, তাই উত্তর ও দক্ষিণ গোলার্ধে সূর্য সমান আলো ফেলে। যে কারণে দিন ও রাতের দৈর্ঘ্য প্রায় সমান হয়।
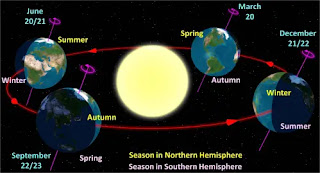
কিন্তু নিচের এই ছবিটাতে (ছবি ৩) আমরা দেখতে পাব এমন সময় আসে যখন পৃথিবীর একটা অংশ সূর্যের দিকে বেশি হেলে পড়ে, কারণ পৃথিবীর ঘূর্ণন অক্ষ ভূকক্ষের দিকে কিছুটা হেলে আছে। তো এই ছবিতে এটা সূর্য, পৃথিবী এই কক্ষপথে ঘুরছে। এই অবস্থানে পৃথিবীর অক্ষরেখা সূর্যের দিকে একটুও হেলে নেই। কিন্তু পৃথিবী ঘুরে যখন এই অবস্থানে আসে তখন সুমেরু অর্থাৎ উত্তর মেরু সূর্যের দিকে বেশি হেলে পড়ে, এবং যথারীতি দক্ষিণ মেরু সূর্য থেকে বেশ খানিকটা দূরে সরে যায়। এ কারণে উত্তর গোলার্ধে এখন গ্রীষ্মকাল আর দক্ষিণ গোলার্ধে শীতকাল। এ সময় তাই উত্তর গোলার্ধে দিনের দৈর্ঘ্য বেশি হয়। এখানে দীর্ঘতম দিন আসে ২১ জুন তারিখে। এখানে ঠিক ২১শে জুনের অবস্থানটাই দেখানো হয়েছে। আবার পৃথিবী ঘুরতে ঘুরতে যখন এই অবস্থানে আসে তখন উল্টো ব্যাপার ঘটে, দক্ষিণ গোলার্ধ সূর্যের দিকে হেলে থাকে বলে সেখানে গ্রীষ্মকাল হয়, উত্তর গোলার্ধে হয় শীতকাল। এ সময় উত্তর গোলার্ধে দিনের দৈর্ঘ্য ছোট হয়, অর্থাৎ এটা ডিসেম্বর মাসের অবস্থান বোঝাচ্ছে।
এই যে পৃথিবীর মেরুগুলো কখনও সূর্যের দিকে আবার কখনও সূর্য থেকে দূরে সরে যাচ্ছে, এর কারণেই পৃথিবীর আকাশে সূর্যকে কখনও উত্তরে আবার কখনও দক্ষিণে দেখা যায়। যেমন মে-জুন মাসে সূর্য থাকে উত্তর গোলার্ধে অর্থাৎ উত্তর গোলার্ধে সে লম্বালম্বিভাবে আলো দেয়। আর আমরা যতোই নভেম্বর-ডিসেম্বরের দিকে যেতে থাকি সূর্য ততোই আকাশের উত্তর থেকে দক্ষিণের দিকে যেতে থাকে, ডিসেম্বর মাসে সে দক্ষিণ গোলার্ধের উপর লম্বালম্বিভাবে আলো দেয়। অন্যদিকে এটা মার্চ মাস, এ সময় সূর্য একেবারে বিষুবরেখার উপরে থাকে, আবার এটা সেপ্টেম্বর মাস, এ সময়ও সূর্য বিষুবরেখার উপর লম্বালম্বিভাবে আলো দেয়। তাহলে ব্যাপারটা দাঁড়াচ্ছে এমন- এই মার্চ থেকে যতোই জুনের দিকে যাওয়া যায় সূর্য বিষুবরেখা থেকে ততোই উত্তরের দিকে যেতে থাকে, ২১শে জুন তারিখে উত্তর দিকে সর্বোচ্চ বিন্দুতে পৌঁছে, তারপর আবার দক্ষিণে যেতে থাকে, সেপ্টেম্বরে আবার বিষুব রেখায় ফিরে আসে, তারপর আরও দক্ষিণে যেতে যেতে ডিসেম্বরে দক্ষিণতম বিন্দুতে পৌঁছায়, তারপর আবার উত্তরের দিকে যেতে শুরু করে।
তো উত্তর এবং দক্ষিণের এই সর্বোচ্চ বিন্দু দুটো কি সেটা আগের ছবিটাতে (ছবি ১) দেখা যাবে। পৃথিবী এখন যেখানে আছে সেটা বসন্ত বিষুব। এখান থেকে যতোই জুন মাসের দিকে যাব সূর্যপথ ততোই বিষুবরেখা অর্থাৎ খ-বিষুব থেকে উত্তরের দিকে যাবে। ঠিক যখন এখানে আসব অর্থাৎ যখন ২১শে জুন আসবে তখন সূর্যের অবস্থান হবে এখানে, বা এই ছবিতে (ছবি ২) এখানে। এখানে বিষুবরেখা থেকে সূর্যের দূরত্ব সবচেয়ে বেশি, অর্থাৎ ২৩.৪ ডিগ্রি। উত্তর দিকে সূর্যের সর্বোচ্চ উন্নতির বিন্দু এটাই, সূর্যের এখানে পৌঁছানোর ঘটনাকে বলা হয় কর্কট ক্রান্তি। আর এ কারণেই পৃথিবীর বিষুবরেখার ঠিক ২৩.৪ ডিগ্রি উত্তরে বিষুবরেখার সমান্তরালে যে বৃত্তটা আঁকা হয় তার নাম কর্কট ক্রান্তি রেখা। কারণ যখন নামটা দেয়া হয়েছিল তখন এই সময় সূর্য খ-গোলকে কর্কট রাশিতে উদিত হতো। তো ঠিক উল্টো ব্যাপার ঘটে ডিসেম্বর মাসে, তখন সূর্য বিষুবরেখার দক্ষিণ দিকে ২৩.৪ ডিগ্রি রেখায় পৌঁছায় যার নাম মকর ক্রান্তি রেখা। এই ছবি থেকে স্পষ্টই বোঝা যাচ্ছে যে ঘূর্ণন অক্ষ ২৩.৪ ডিগ্রি হেলে থাকার কারণেই এই ক্রান্তিগুলো ঘটছে। এ কারণেই ২৩.৪ ডিগ্রি কোণটাকে বলা হয় ক্রান্তিকোণ।
তো এরাটোস্থেনিসের পৃথিবীর পরিধি নির্ণয় বোঝাতে গিয়ে অনেক কথা বলে ফেললাম, কিন্তু এই ব্যাপারটা পুরো না বুঝলে এরাটোস্থেনিসের পদ্ধতি বোঝা সম্ভব না। তিনি কর্কট ক্রান্তি ব্যবহার করে পরিধি পরিমাপ করেছিলেন। সুতরাং কর্কট ক্রান্তিতে কি ঘটে সেটা আরেকটু পরিষ্কারভাবে দেখা যাক, এই ছবিতে (ছবি ৪)। এখানে বিষুব, কর্কট ও মকর ক্রান্তি রেখা দেখা যাচ্ছে। আর পৃথিবীর এই অবস্থানটা ঠিক ২১শে জুন তারিখের, অর্থাৎ কর্কট ক্রান্তির। এ সময় সূর্য বিষুবরেখার উত্তরে ২৩.৪ ডিগ্রি অক্ষাংশে পৌঁছায়। এগুলো সূর্যের রশ্মি। সূর্য পৃথিবী থেকে এতো দূরে যে তার কিরণ যখন পৃথিবীতে আসে তখন তারা একে অপরের একেবারে সমান্তরাল থাকে। পৃথিবীর সব জায়গাতেই দেখা যাচ্ছে সমান্তরালভাবে সূর্যের আলো পড়ছে, এই ব্যাপারটাও এরাটোস্থেনিস বুঝতে পেরেছিলেন, ঠিক এ কারণেই পরিধিটা মাপতে পেরেছিলেন। তো দেখা যাচ্ছে, কর্কট ক্রান্তিতে যদি কোন ব্যক্তি ঠিক কর্কট ক্রান্তি রেখার উপর দাঁড়ায়– আগেই বলে রাখি কর্কট ক্রান্তি হচ্ছে ২১শে জুনের ঘটনাটা আর কর্কট ক্রান্তি রেখা হচ্ছে বিষুবরেখার ২৩.৪ ডিগ্রি উত্তরের সমান্তরাল বৃত্তটা– তো সে যদি ঠিক ভরদুপুড়ে এখানে দাঁড়ায় তাহলে তার মাথা থাকবে সোজা এই দিকে, যেদিক থেকে সূর্যের আলো পড়ছে। সুতরাং তার কোন ছায়া পড়বে না। আসলে মানুষের ক্ষেত্রে হয়তো হাতের ছায়া নিচে দেখা যাবে। কিন্তু এখানে যদি ভূপৃষ্ঠের সাথে লম্বভাবে একটা লাঠি পোঁতা হয় তাহলে তার কোন ছায়াই পড়বে না। অবশ্যই ভরদুপুড়ের আগে-পড়ে ছায়া পড়বে কারণ তখন সূর্য পূর্ব বা পশ্চিম দিকে থাকবে। কিন্তু ভরদুপুড়ে সূর্য থাকবে লাঠিটার ঠিক উপরে, তাই ছায়া পড়বে না। কিন্তু এই একই দিনের একই সময়ে কর্কট ক্রান্তি রেখা থেকে আরও উত্তরে গেলে কিন্তু ছায়া পড়বে।
তো এরাটোস্থেনিস থাকতেন কর্কট ক্রান্তি রেখা থেকে আরও উত্তরে, আলেকজান্দ্রিয়া শহরে। আলেকজান্দ্রিয়ার অবস্থান মানচিত্রে এখানে। তিনি ছিলেন আলেকজান্দ্রিয়ার গ্রন্থাগারের গ্রন্থাগারিক। তো গ্রন্থাগারে বই পড়তে পড়তে হঠাৎ তিনি দেখলেন একটা বইয়ে লেখা আছে, ২১শে জুন তারিখের ঠিক ভরদুপুড়ে মিশরের সায়িন নামক স্থানে কোন বস্তুর ছায়া পড়ে না। আসলে আলেকজান্দ্রিয়া থেকে দক্ষিণে যেতে থাকলে সায়িনই বোধহয় প্রথম জায়গা যেখানে এই ছায়াহীনতার ব্যাপারটা ঘটে। এতোক্ষণে নিশ্চয়ই বুঝতে পেরেছেন সায়িন কর্কট ক্রান্তি রেখার উপরে আছে। এই রেখাটা বাংলাদেশেরও উপর দিয়ে গেছে। এখানে বাংলাদেশ, আর সায়িন হবে এখানে। তো এরাটোস্থেনিস জানেন সেই একই দিনের একই সময়ে আলেকজান্দ্রিয়াতে ছায়া পড়ে। ছায়ার দৈর্ঘ্যের এই পার্থক্য থেকে তিনি পরিধি মাপেন, কিভাবে করেন সেটা বোঝানোর আগে একটা সিম্যুলেশনের মাধ্যমে প্রমাণ করে নেয়া যাক যে আসলেই সায়িনে ছায়া পড়ে না কিন্তু আলেকজান্দ্রিয়াতে পড়ে।
এবার ২১শে জুনের ঠিক ভরদুপুড়ে সায়িনের সূর্যটা দেখা যাক। আমরা পুরো দিনটাই দেখি। দিন হবে ২১শে জুন, সময় দেই রাত তিনটা, আর এখানে সায়িনের অক্ষাংশটা দিতে হবে। আনুমানিক ২৪ ডিগ্রি দিলাম।এবার রান করাই, দেখতে পাচ্ছি সূর্য উদিত হচ্ছে, লম্বা ছায়া দেখা যাচ্ছে। এই এখানে ঠিক ভরদুপুড়ে কোন ছায়া নেই। তারপর আবার ছায়া লম্বা হচ্ছে। আসলে মানুষের এই অংশের ছায়াপ ঠিক নিচে দেখা যাচ্ছে ভরদুপুড়েও। কিন্তু এখানে একটা লাঠি পোতা হলে একদমই কোন ছায়া পড়তো না। যাহোক এখন এই একই দিনের একই সময়ে আলেকজান্দ্রিয়ার অবস্থা দেখা যাক। আমরা এখন জানি এই শহরে অক্ষাংশ ৩১ ডিগ্রি। সেটা দিয়ে দেই। এবার রান করাই। দেখতে পাচ্ছি পুরো দিন জুড়েই ছায়া আছে। শুধু ভরদুপুড়ের মুহূর্তটা তুলনা করা যাক। আলেকজান্দ্রিয়াতে ২১শে জুনের ভরদুপুড়ে ছায়া আছে কিন্তু সায়িনে নেই।
ছবিতে দেখা যাচ্ছে, সূর্যরশ্মি AB আর CD সমান্তরাল। ফলে এদের একান্তর কোণদুটি ∠DCA আর পৃথিবীর কেন্দ্রে ∠CAB সমান। এভাবে কাঠি আর ছায়ার দৈর্ঘ্য দেখে কোণ হিসাব করে ফেললেন ইরাটোস্থেনিস। দেখা গেল এই কোণ বৃত্তের কোণের পঞ্চাশ ভাগের এক ভাগ (৩৬০° কোণের পঞ্চাশ ভাগের এক ভাগ)। তখনকার সময়ে আলেক্সান্দ্রিয়াতে দূরত্ব মাপা হতো স্টেডিয়া এককে। সাইন আর আলেক্সান্দ্রিয়ার দূরত্ব ছিল প্রায় ৫,০০০ স্টেডিয়া। এখন খুব সহজভাবে চিন্তা করা যাক।
এটা পৃথিবীর কেন্দ্র, পৃথিবীটা ছবি থেকে উঠিয়ে দিলে আমরা দেখব- লাঠি দুটোকে যদি পেছনের দিকে বাড়িয়ে দেয়া হয় তাহলে তারা অবশ্যই পৃথিবীর কেন্দ্রে গিয়ে ছেদ করবে। আলেকজান্দ্রিয়া ও সায়িনের লাঠিদুটো পৃথিবীর কেন্দ্রে যে কোণ উৎপন্ন করবে সেটা অবশ্যই এরাটোস্থেনিসের নির্ণীত এই কোণের সমান হবে। কারণ দেখা যাচ্ছে এই রেখা দুটো পরষ্পরের সমান্তরাল, এই রেখাটা দুটো সমান্তরাল রেখাকে ছেদ করেছে। তাহলে সূত্র অনুসারে এই কোণ অবশ্যই এই কোণের সমান। তার মানে আলেকজান্দ্রিয়া থেকে সায়িন পর্যন্ত একটা বৃত্তচাপ আঁকলে তা বৃত্তের কেন্দ্রে যে কোণ তৈরি করবে সেটা আমরা পেয়ে গেলাম। আমরা জানি পুরো বৃত্তের কোণ ৩৬০ ডিগ্রি। আর এটুকুর কোণ এখানে লেখা আছে ৭.২ ডিগ্রি। তাহলে পুরো বৃত্ত এটুকুর সাপেক্ষে কত বড় সেটা ক্যালকুলেটর দিয়ে খুব সহজেই নির্ণয় করে ফেলা যায়। করেই ফেলি। ৩৬০ ভাগ ৭.২ পাওয়া যাচ্ছে ৫০। অর্থাৎ আলেকজান্দ্রিয়া ও সায়িনের কৌণিক দূরত্ব একটি পৃথিবী বৃত্তের মোট কোণের ৫০ ভাগের ১ ভাগ। তাহলে আলেকজান্দ্রিয়া ও সায়িনের রৈখিক দূরত্বও পৃথিবীর পরিধির ৫০ ভাগের ১ ভাগ হবে। এখন শুধু এই দূরত্বটা জানা দরকার। এরাটোস্থেনিস একজন লোক ভাড়া করলেন আলেকজান্দ্রিয়া থেকে সায়িন পর্যন্ত দূরত্ব মাপতে। তখন মিশরে স্ট্যাডিয়ন নামে একটা একক ব্যবহার করা হতো। দূরত্বটা সেই এককেই মাপা হয়েছিল। আমরা অতো ঝামেলায় যাব না। সেই দূরত্বকে কিলোমিটারে রূপান্তর করলে পাওয়া যায় আনুমানিক ৮০০ কিলোমিটার। এটাকে যদি ৫০ দিয়ে গুণ করি তাহলেই পুরো পৃথিবীর পরিধি পাওয়া যাবে। ৮০০ গুণ ৫০ সমান ৪০ হাজার কিলোমিটার।
বৃত্তের পঞ্চাশ ভাগের এক ভাগের জন্য দূরত্ব হয় ৫,০০০ স্টেডিয়া। তাহলে পুরো বৃত্তের জন্য দূরত্ব (যার নাম পরিধি) হবে এর ৫০ গুণ, মানে ২৫,০০০ স্টেডিয়া, কিলোমিটারের হিসাবে যা প্রায় ৩৯,৬৯০ কিলোমিটার। আজ আমরা জানি পৃথিবীর পরিধি (এটি বৃত্তের পরিধি, গোলকের ক্ষেত্রফল না) প্রায় ৪০,২০০ কিলোমিটারের মতো। অর্থাৎ এত বছর আগেও ইরাটোস্থেনিসের হিসাবে ভুলের পরিমাণ ছিল ২ শতাংশেরও কম!
এরাটোস্থেনিস পৃথিবীর পরিধি পেয়েছিলেন ৪০ হাজার কিলোমিটার। এটা আসল মানুর খুবই কাছাকাছি। আমরা শুধু ধারণা দেয়ার জন্য যখন কাউকে পৃথিবীর পরিধি বলি তখন ৪০ হাজার কিলোমিটারই বলি। আজ থেকে ২২০০ বছর পূর্বে এরাটোস্থেনিস এটা নির্ণয় করে ফেলেছিলেন। তার খুব আধুনিক কোন প্রযুক্তিই লাগেনি। তিনি ব্যবহার করেছিলেন কেবল একটা লাঠি, একটা দড়ি আর তার মস্তিষ্ক। তবে সবচেয়ে বড় কথা তার পরীক্ষা-নীরিক্ষা ও পর্যবেক্ষণের প্রতি অগাধ বিশ্বাস ও নির্ভরতা ছিল, যেটা বিজ্ঞানের মূলমন্ত্র
এখানে আরেকটা বিষয় উল্লেখ করা যায়। ক্লিওমেডের বইতে পাওয়া যায়, পৃথিবীর পরিধি ২৫,০০০ স্টেডিয়া। আরেকদল ইতিহাসবেত্তার দাবি, ইরাটোস্থেনিসের মূল পরীক্ষায় এই মান ছিল ২৫,২০০ স্টেডিয়া। অনেকের ধারণা, গ্রীক দার্শনিকদের মধ্যে সংখ্যা বিষয়ক কিছু বাড়াবাড়ি আবেগ দেখা যায়। ২৫,২০০ সংখ্যাটি ১ থেকে ১০ এর ভেতর সবগুলো স্বাভাবিক সংখ্যা দিয়ে নিঃশেষে বিভাজ্য বলেই ইচ্ছাকৃতভাবে ইরাটোস্থেনিস কাছাকছি এই সংখ্যাটি বেছে নিয়েছিলেন বলে অনেকে মনে করেন। তবে এর পক্ষে-বিপক্ষে সেরকম শক্তিশালী দলিল পাওয়া যায় না।
References :
1)https://bn.wikipedia.org/wiki/%E0%A6%8F%E0%A6%B0%E0%A6%BE%E0%A6%A4%E0%A7%8B%E0%A6%B8%E0%A7%8D%E0%A6%A5%E0%A7%87%E0%A6%A8%E0%A7%87%E0%A6%B8
2)

.webp)